4. Rectangular directional coupler

In this example we model a cross-section of a \(2\times 2\) directional coupler formed from rectangular strip-loaded waveguides. Parameters were taken from this guide. First, I’ll construct the waveguide.

from wavesolve.waveguide import Rectangle,Waveguide

airclad = Rectangle(1.,"air")
airclad.make_points(-12,12,-16,8)

strip1 = Rectangle(1.45,"strip1")
strip1.make_points(-5.5,-0.5,0,2)

strip2 = Rectangle(1.45,"strip2")
strip2.make_points(0.5,5.5,0,2)

corelayer = Rectangle(1.77,"corelayer")
corelayer.make_points(-10,10,-1,0)

clad = Rectangle(1.45,"clad")
clad.make_points(-10,10,-10,-1)

strip1.mesh_size = 1.0
strip2.mesh_size = 1.0
clad.mesh_size = 1.0
corelayer.mesh_size = 0.25

wvg = Waveguide([airclad,[strip1,strip2,corelayer,clad]] )
m = wvg.make_mesh(order=1)

wvg.plot_mesh(m,plot_points=False)

(Source code, png, hires.png, pdf)

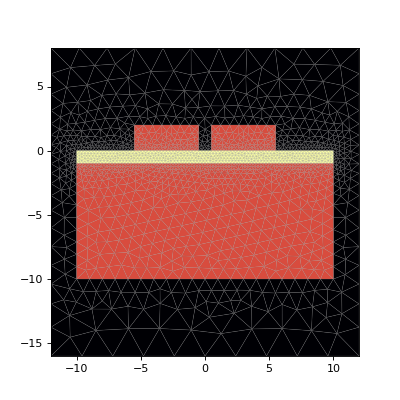
Next, we’ll solve and look for the TM₀₀ modes, which will be vertically polarized.

from wavesolve.FEsolver import solve_waveguide_vec,plot_vector_field,get_eff_index
import matplotlib.pyplot as plt

wl = 1.
IOR_dict = wvg.assign_IOR()

w,v = solve_waveguide_vec(m,wl,IOR_dict,Nmax = 8)

ne = get_eff_index(wl,w)

fig,axs = plt.subplots(8,1,sharex=True,sharey=True,figsize=(8,12))
for i,ax in enumerate(axs.flatten()):
    ax.set_title("mode "+str(i+1)+r": $n_{\rm eff}=$"+str(round(np.real(ne[i]),5)))
    plot_vector_field(m,v[i],ax=axs.flatten()[i],bounds=(-10,10,-2,1))
    wvg.plot_boundaries(ax)
plt.show()

(Source code, png, hires.png, pdf)

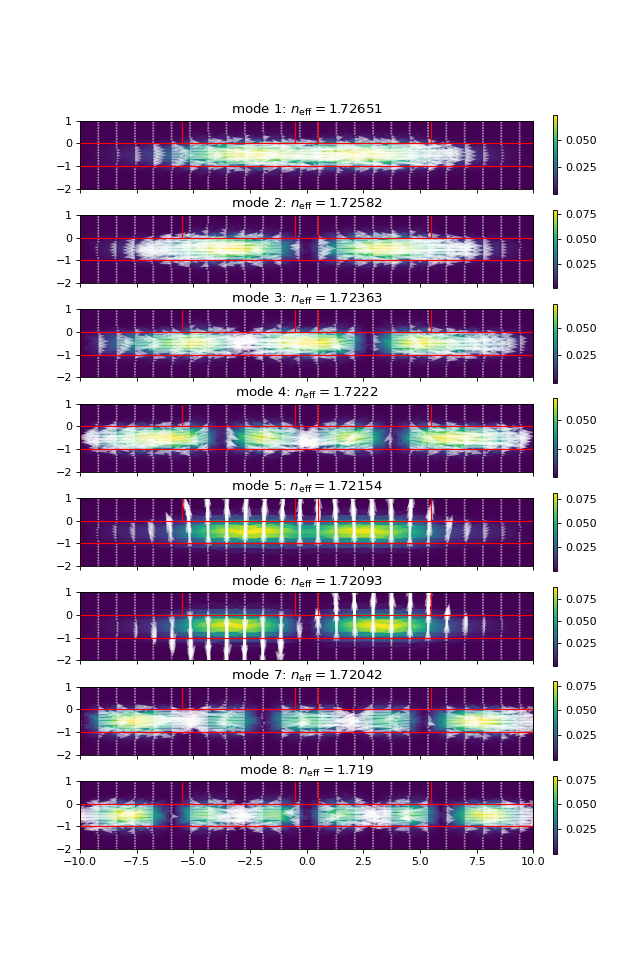
From these plots, we can see that modes 5 and 6 are our first two TM₀₀ modes. The coupling length is given by

\[L_c = \dfrac{\lambda}{2(n_{\rm eff,1}-n_{\rm eff,2})}.\]

I find a coupling length of around 820 \(\mu\)m, which is quite close to the 811 \(\mu\)m value quoted by the guide I referenced.